课题背景

这次课题选择是Digit Recognizer^[1]，本课题是kaggle上的一个简单的机器学习任务。此任务内容是在MNIST^[2]（Modified National Institute of Standards and Technology）数据集上训练一个数字识别器。MINIST是一个用于计算机视觉处理入门型的数据集。

数据集为两部分，首先是训练集，本课题的大小为42000个样本，每个样本是0~9的分类和28*28=784个灰度像素值，分别表示数字和对应的手写数字的图像。其次还有个大小为20000个样本的测试集，测试集的样本只包含像素值，不包含分类。

通过训练集训练模型，再使用模型去处理测试集，从而得到测试结果。测试结果包含像素值所表示图像ID（即下标）以及像素值所表示的数字。最后在kaggle上的排名以在测试集合上的分类正确率为依据。

手写数字识别是一种常见的应用场景，典型的例如网站验证码的识别。并由此可推广至文字识别、文档OCR识别这种传统的普遍应用，乃至车牌交通标识识别、新型人机交互系统等等更智能化的应用。故此课题的研究虽然简单，但有广泛的应用价值。

算法背景

根据本任务页面的描述，使用神经网络、SVM以及K-近邻算法可以得到比较好的处理结果。再结合时间公司培训内容，遂选择SVM作为本次课题的主要算法。

SVM简介

SVM（support vector machine支持向量机）^[3]是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。如图1：

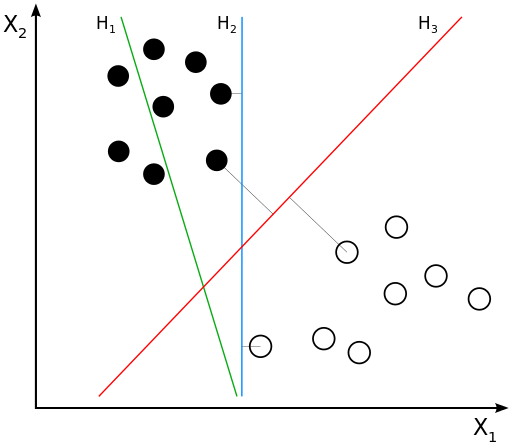
File:Svm separating hyperplanes (SVG).svg

图1：H1不能把类别分开。H2可以，但只有很小的间隔。

H3以最大间隔将它们分开。

线性SVM

我们考虑以下形式的点测试集：

其中是1或者−1，表明点所属的类。中每个都是一个维实向量。我们要求将的点集与的点集分开的“最大间隔超平面”，使得超平面与最近的点之间的距离最大化。

任何超平面都可以写作满足下面方程的点集

其中（不必是归一化的）是该法向量。参数决定从原点沿法向量到超平面的偏移量。

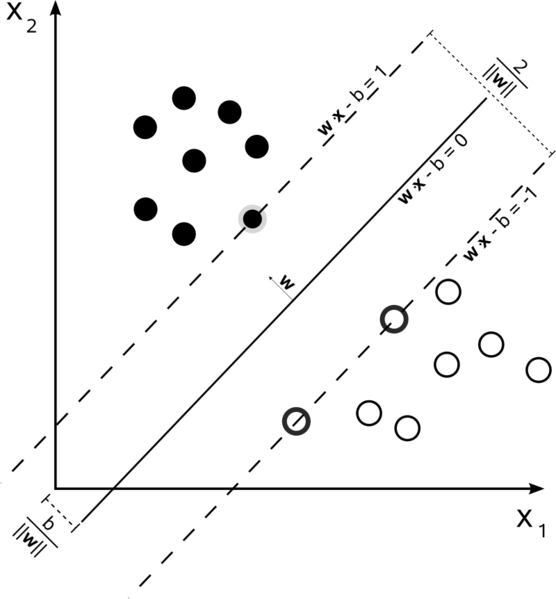
File:Svm max sep hyperplane with margin.png

图2：设样本属于两个类，用该样本训练SVM得到的最大间隔超平面。在超平面上的样本点也称为支持向量。

硬间隔

如果这些训练数据是线性可分的，可以选择分离两类数据的两个平行超平面，使得它们之间的距离尽可能大。在这两个超平面范围内的区域称为“间隔”，最大间隔超平面是位于它们正中间的超平面。这些超平面可以由方程族：

或是来表示。

通过几何不难得到这两个超平面之间的距离是，因此要使两平面间的距离最大，我们需要最小化。同时为了使得样本数据点都在超平面的间隔区以外，我们需要保证对于所有的满足其中的一个条件：

若或是若

这些约束表明每个数据点都必须位于间隔的正确一侧。

这两个式子可以写作：

可以用这个式子一起来得到优化问题：

“在条件下，最小化，对于 ”

这个问题的解与决定了我们的分类器

此几何描述的一个显而易见却重要的结果是，最大间隔超平面完全是由最靠近它的那些确定的。这些叫做支持向量。

软间隔

为了将SVM扩展到数据线性不可分的情况，我们引入损失函数，

当约束条件(1)满足时（也就是如果位于边距的正确一侧）此函数为零。对于间隔的错误一侧的数据，该函数的值与距间隔的距离成正比。然后我们希望最小化

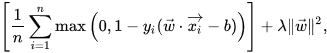
其中参数用来权衡增加间隔大小与确保位于间隔的正确一侧之间的关系。因此，对于足够小的值，如果输入数据是可以线性分类的，则软间隔SVM与硬间隔SVM将表现相同，但即使不可线性分类，仍能学习出可行的分类规则。

核函数

尽管原始问题可能是在有限维空间中陈述的，但用于区分的集合在该空间中往往线性不可分。为此，有人提出将原有限维空间映射到维数高得多的空间中，在该空间中进行分离可能会更容易。为了保持计算负荷合理，人们选择适合该问题的核函数来定义SVM方案使用的映射，以确保用原始空间中的变量可以很容易计算点积。如图2：

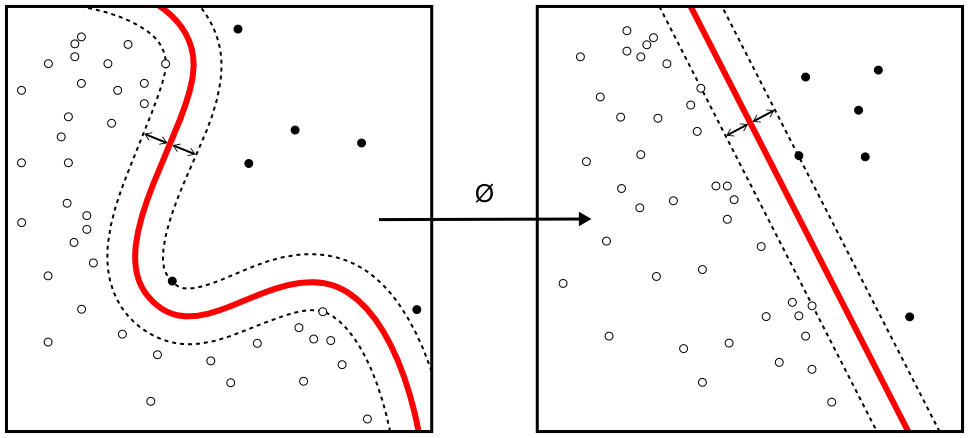
图2：核函数示意图

高维空间中的超平面定义为与该空间中的某向量的点积是常数的点的集合。值得注意的是，更高维的特征空间增加了支持向量机的泛化误差，但给定足够多的样本，算法仍能表现良好。

主要参数

SVM的有效性取决于核函数、核参数和软间隔参数C的选择。核函数通常会选只有一个核参数γ的高斯函数。C和γ的最佳组合通常通过在C和γ为指数增长序列下网格搜索来选取。通常情况下，使用交叉验证来检查参数选择的每一个组合，并选择具有最佳交叉验证精度的参数。或者把随机搜索用于选择C和γ，通常需要评估比网格搜索少得多的参数组合。然后，使用所选择的参数在整个训练集上训练用于测试和分类新数据的最终模型。

整体思路

本课题整体思路分为以下几步骤：

数据读入
定制数据处理流程
1. 选择PCA用于后续数据对齐处理
2. 选择SVM用于后续模型训练
3. 使用Pipeline^[4]定制PCA和SVM的处理流程
设置参数搜索
1. 开始使用大范围参数配合随机搜索
2. 随后使用确定数目的固定参数集进行网格搜索
3. 最终使用确定参数
训练模型
1. 开始使用随机搜索验证^[5]来确定大体范围
2. 随后使用网格搜索验证^[6]来确定详细范围
3. 最终使用确定参数训练
预测测试数据
输出结果
提交kaggle验证结果有效性
重复3-7部分以求kaggle得分高

数据处理说明

概要说明

在计算模型训练前，我们需要对原始数据进行处理以适合进行训练。在数据处理部分使用PCA^[7]（主成分分析）方式对数据进行处理。

PCA顾名思义，即分析数据主要成分来处理数据的方法，其要点为降维处理和白化^[8]。以下分别介绍

降维处理

PCA的降维处理方式为：通过计算出n个维度训练数据矩阵的协方差矩阵∑，其大小为n*n。我们先计算出协方差矩阵∑的特征向量，按特征值大小来定位其列排放，而组成特征矩阵

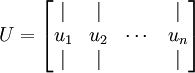$\begin{align} U = \begin{bmatrix} | & | & & | \\ u_1 & u_2 & \cdots & u_n \\ | & | & & | \end{bmatrix} \end{align}$ 此处， $\textstyle u_1$ 是主特征向量（对应最大的特征值）， $\textstyle u_2$ 是次特征向量。以此类推，另记 $\textstyle \lambda_1, \lambda_2, \ldots, \lambda_n$ 从大到小为相应的特征值。

接下来还需要一个旋转的过程。加入我们有一个2维度的数据集，可以把 $\textstyle x$ 用 $\textstyle (u_1, u_2)$ 基表达为：

$\begin{align} x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}$

（下标“rot”来源于单词“rotation”，意指这是原数据经过旋转（也可以说成映射）后得到的结果）

对数据集中的每个样本 $\textstyle i$ 分别进行旋转： $\textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}$ ，这就是把训练数据集旋转到 $\textstyle u_1$ ， $\textstyle u_2$ 基后的结果。一般而言，运算 $\textstyle U^Tx$ 表示旋转到基 $\textstyle u_1$ , $\textstyle u_2$ ,…, $\textstyle u_n$ 之上的训练数据。矩阵 $\textstyle U$ 有正交性，即满足 $\textstyle U^TU = UU^T = I$ ，所以若想将旋转后的向量 $\textstyle x_{\rm rot}$ 还原为原始数据 $\textstyle x$ ，将其左乘矩阵 $\textstyle U$ 即可： $\textstyle x=U x_{\rm rot}$ ,验算一下： $\textstyle U x_{\rm rot} = UU^T x = x$ .

数据的主方向就是旋转数据的第一维 $\textstyle x_{{\rm rot},1}$ 。因此，若想把这数据降到一维，可令：

$\begin{align} \tilde{x}^{(i)} = x_{{\rm rot},1}^{(i)} = u_1^Tx^{(i)} \in \Re. \end{align}$

更一般的，假如想把数据 $\textstyle x \in \Re^n$ 降到 $\textstyle k$ 维表示 $\textstyle \tilde{x} \in \Re^k$ （令 $\textstyle k < n$ ）,只需选取 $\textstyle x_{\rm rot}$ 的前 $\textstyle k$ 个成分，分别对应前 $\textstyle k$ 个数据变化的主方向。

PCA的另外一种解释是： $\textstyle x_{\rm rot}$ 是一个 $\textstyle n$ 维向量，其中前几个成分可能比较大（例如，上例中大部分样本第一个成分 $\textstyle x_{{\rm rot},1}^{(i)} = u_1^Tx^{(i)}$ 的取值相对较大），而后面成分可能会比较小（例如，上例中大部分样本的 $\textstyle x_{{\rm rot},2}^{(i)} = u_2^Tx^{(i)}$ 较小）。

PCA算法做的其实就是丢弃 $\textstyle x_{\rm rot}$ 中后面（取值较小）的成分，就是将这些成分的值近似为零。具体的说，设 $\textstyle \tilde{x}$ 是 $\textstyle x_{{\rm rot}}$ 的近似表示，那么将 $\textstyle x_{{\rm rot}}$ 除了前 $\textstyle k$ 个成分外，其余全赋值为零，就得到：

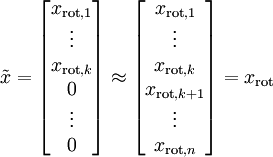
$\begin{align} \tilde{x} = \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \approx \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ x_{{\rm rot},k+1} \\ \vdots \\ x_{{\rm rot},n} \end{bmatrix} = x_{\rm rot} \end{align}$

然而，由于上面 $\textstyle \tilde{x}$ 的后 $\textstyle n-k$ 项均为零，没必要把这些零项保留下来。所以，我们仅用前 $\textstyle k$ 个（非零）成分来定义 $\textstyle k$ 维向量 $\textstyle \tilde{x}$ 。

这也解释了我们为什么会以 $\textstyle u_1, u_2, \ldots, u_n$ 为基来表示数据：要决定保留哪些成分变得很简单，只需取前 $\textstyle k$ 个成分即可。这时也可以说，我们“保留了前 $\textstyle k$ 个PCA（主）成分”。

现在，我们得到了原始数据 $\textstyle x \in \Re^n$ 的低维“压缩”表征量 $\textstyle \tilde{x} \in \Re^k$ ，反过来，如果给定 $\textstyle \tilde{x}$ ，我们应如何还原原始数据 $\textstyle x$ 呢？根据上面的过程可知，要转换回来，只需 $\textstyle x = U x_{\rm rot}$ 即可。进一步，我们把 $\textstyle \tilde{x}$ 看作将 $\textstyle x_{\rm rot}$ 的最后 $\textstyle n-k$ 个元素被置0所得的近似表示，因此如果给定 $\textstyle \tilde{x} \in \Re^k$ ，可以通过在其末尾添加 $\textstyle n-k$ 个0来得到对 $\textstyle x_{\rm rot} \in \Re^n$ 的近似，最后，左乘 $\textstyle U$ 便可近似还原出原数据 $\textstyle x$ 。具体来说，计算如下：

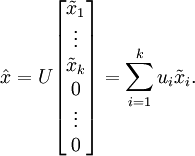
$\begin{align} \hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}$

上面的等式基于先前对 $\textstyle U$ 的定义。在实现时，我们实际上并不先给 $\textstyle \tilde{x}$ 填0然后再左乘 $\textstyle U$ ，因为这意味着大量的乘0运算。我们可用 $\textstyle \tilde{x} \in \Re^k$ 来与 $\textstyle U$ 的前 $\textstyle k$ 列相乘，即上式中最右项，来达到同样的目的。

在训练自动编码器或其它无监督特征学习算法时，算法运行时间将依赖于输入数据的维数。若用 $\textstyle \tilde{x} \in \Re^k$ 取代 $\textstyle x$ 作为输入数据，那么算法就可使用低维数据进行训练，运行速度将显著加快。对于很多数据集来说，低维表征量 $\textstyle \tilde{x}$ 是原数据集的极佳近似，因此在这些场合使用PCA是很合适的，它引入的近似误差的很小，却可显著地提高你算法的运行速度。

通过降维可以使得数据训练过程加快，但降维太少则起不到加速效果，降维太多则损失数据精度。我们需要一个容易掌握的调整的值来表示我们需要降到多少维度，以衡量处理不同维度的数据的维度保留情况。这里可以通过控制保留方差的方式来控制选择剩余维度个数。保留方差的计算公式为

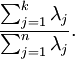$\begin{align} \frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}. \end{align}$ 即保留的维度的特征值之和除以全部特征值和。该值的范围是[0,1]。若取值0.9，则可以理解为保留了最主要的90%的特征。在本课题中代码的components参数即代表该值。

白化

我们上面已经了解了如何使用PCA降低数据维度。在执行算法中还需要一个与之相关的预处理步骤，这个预处理过程称为白化。以当前课题举例，训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：

特征之间相关性较低；
所有特征具有相同的方差。

白化的公式很简单 $\begin{align} x_{{\rm PCAwhite},i} = \frac{x_{{\rm rot},i} }{\sqrt{\lambda_i}}. \end{align}$ ，具体思想如下：

如何消除输入特征之间的相关性?在前文计算 $\textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}$ 时实际上已经消除了输入特征 $\textstyle x^{(i)}$ 之间的相关性。

对于维度为2的数据来说，其协方差矩阵如下：

$\textstyle \lambda_1$ 0

0 $\textstyle \lambda_2$

$\textstyle x_{\rm rot}$ 协方差矩阵对角元素的值为 $\textstyle \lambda_1$ 和 $\textstyle \lambda_2$ 绝非偶然。并且非对角元素值为0;因此, $\textstyle x_{{\rm rot},1}$ 和 $\textstyle x_{{\rm rot},2}$ 是不相关的,满足我们对白化结果的第一个要求(特征间相关性降低)。

为了使每个输入特征具有单位方差，我们可以直接使用 $\textstyle 1/\sqrt{\lambda_i}$ 作为缩放因子来缩放每个特征 $\textstyle x_{{\rm rot},i}$ 。具体地，我们定义白化后的数据 $\textstyle x_{{\rm PCAwhite}} \in \Re^n$ 如下：

$\begin{align} x_{{\rm PCAwhite},i} = \frac{x_{{\rm rot},i} }{\sqrt{\lambda_i}}. \end{align}$
这些数据现在的协方差矩阵为单位矩阵 $\textstyle I$ 。我们说， $\textstyle x_{{\rm PCAwhite}}$ 是数据经过PCA白化后的版本: $\textstyle x_{{\rm PCAwhite}}$ 中不同的特征之间不相关并且具有单位方差。

本课题中全部代码默认开启白化来处理数据。

算法及代码

鉴于调整参数时代码基本重复，故只给出首次随机搜索时代码如下：

import pandas as pd
import numpy as np
import time
import random
import matplotlib.pyplot as plt
#pca
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline
#svc
from sklearn.svm import SVC,NuSVC
from sklearn.model_selection import  GridSearchCV,RandomizedSearchCV
#显示结果样例
def plot_sample(test_data, result, count=20):
    sample = random.sample(range(0,result.shape[0]),count)
    fig = plt.figure(figsize=[16,9])
    #plt.title("Test Data Sample", fontsize=20, color="b")
    plt.xticks([])
    plt.yticks([])
    plt.axis('off')
    i = 0
    for pos in sample:
        p1 = fig.add_subplot(4,(count/4)+(count%4), i+1)
        title_str="Result: "+str(result[pos])
        plt.title(title_str)
        grid_data = test_data[pos].reshape(28,28) 
        p1.imshow(grid_data, cmap = plt.cm.gray_r)
        i = i+1
        plt.xticks([])
        plt.yticks([])
    plt.show()
def write(clf, test_data):
    start = time.clock()
    result=clf.predict(test_data)
    result = np.c_[range(1,len(result)+1), result.astype(int)]
    df_result = pd.DataFrame(result, columns=['ImageId', 'Label'])
    df_result.to_csv('./data/results.csv', index=False)
    elapsed = (time.clock() - start)
    print("Test Time used:",elapsed)
    plot_sample(test_data, result)
if __name__=='__main__':
    #read data
    start = time.clock()
    X_test = pd.read_csv("./data/test.csv").values
    dataset = pd.read_csv("./data/train.csv")
    X_train = dataset.values[0:, 1:]
    y_train = dataset.values[0:, 0]
    #for fast evaluation
    X_train_small = X_train[:10000, :]
    y_train_small = y_train[:10000]
    #plot_sample(X_train, y_train)
    elapsed = (time.clock() - start)
    print("Read Time used:",elapsed)
   
    #begin progressing
    start = time.clock()
    parameters = dict(
        pca__n_components = np.arange(0.7,0.99,0.05),
        svc__gamma = np.arange(0.01,0.1, 0.02),
        svc__kernel = ['linear', 'rbf'],
        svc__C = np.arange(1,50,5) )
    pipe_clf=Pipeline([('pca', PCA(whiten=True)), ('svc', SVC())])
    
    #fast search
    rs_clf = RandomizedSearchCV(pipe_clf, parameters, n_jobs=-1, verbose=True )
    rs_clf.fit( X_train_small, y_train_small )
    elapsed = (time.clock() - start)
    print("Train Time used:",elapsed)

    print()
    #for params, mean_score, std_scores in rs_clf.grid_scores_:
    #    print("%0.3f (+/-%0.03f) for %r"  % (mean_score, std_scores.std() * 2, params))
    print("Best:", rs_clf.best_params_ , rs_clf.best_score_)
    #test & write
    write(rs_clf, X_test)
    exit(0)

图表和结果展现

运行环境

项目	参数
CPU	Intel Core i7-3720QM CPU@2.60GHz 4 Cores 8 Threads
MEMORY	8GB DDR3 x 2@1600Mhz
HD	256GB SSD
OS	Windows 10 Pro 64bit
IDE	Visual Studio 2017+Anaconda 5.0+Python 3.6 64bit

运行结果

第一次随机搜索
1. 控制台输出

Fitting 3 folds for each of 10 candidates,totaling 30 fits

[Parallel(n_jobs=-1)]:Done 30 out of 30|elapsed:1.7min finished

Train Time used:108.23998763676728

……

Best:{‘svc__kernel’:’rbf’,’svc__gamma’:0.029999999999999999,’svc__C’:36,’pca__n_components’:0.75} 0.9672

Test Time used:6.136322404056656

1. Kaggle结果

最终训练

图形效果

每次程序运行完毕时，会有一个图形样例的输出如下：

$C:\Users\davel\Desktop\Figure_1.png$

参考文档

Digit Recognizer https://www.kaggle.com/c/digit-recognizer
MINST http://yann.lecun.com/exdb/mnist/
SVM https://en.wikipedia.org/wiki/Support_vector_machine
Pipeline http://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html
RandomizedSearchCV http://scikit-learn.org/stable/modules/generated/sklearn.grid_search.RandomizedSearchCV.html
GridSearchCV http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html
PCA http://ufldl.stanford.edu/wiki/index.php/PCA
白化 http://ufldl.stanford.edu/wiki/index.php/Whitening

8 Responses to kaggle数字识别器训练过程

kn007 says:

2018/02/01 at 17:23

看到算法，瞬间一脸懵逼。。。完全不懂。

回复
大D says:

2018/02/02 at 15:53

先码后看

回复
daozhihun says:

2018/02/05 at 17:17

贴的这些公式，在具体应用的时候真的会去看和计算么？还是只是吹牛逼用的啊～

回复
- davelv says:
  
  2018/03/18 at 03:23
  
  公式是原理，实际使用中并不会用到，但是会影响你使用的效果。
  就像在用std::map时候你可以不用知道它是红黑树做的，而如果你知道了，你就可以清楚它适合做什么。
  
  回复
  - daozhihun says:
    
    2018/03/23 at 13:42
    
    dave在网上和私底下说话给人的感觉不一样～
    在网上有一种为人师表的赶脚～
    
    回复
    - davelv says:
      
      2018/03/25 at 23:03
      
      哈哈，可能是受到父母的影响。
      也可能做个教师也很适合我
      
      回复
adamfei says:

2018/02/08 at 10:52

时隔四年半，D大终于更新了，遥想那会我才刚毕业工作啊……感慨时光流逝！最后祝D大小年快乐。

回复
- davelv says:
  
  2018/05/04 at 16:52
  
  五四青年节快乐！
  
  回复

System C.

程序设计=数据结构+算法

kaggle数字识别器训练过程

课题背景

算法背景

SVM简介

线性SVM

硬间隔

软间隔

核函数

主要参数

整体思路

数据处理说明

概要说明

降维处理

白化

算法及代码

图表和结果展现

运行环境

运行结果

参考文档

8 Responses to kaggle数字识别器训练过程

发表回复取消回复

近期评论

近期文章

朋友们

分类目录

归档

课题背景

算法背景

SVM简介

线性SVM

硬间隔

软间隔

核函数

主要参数

整体思路

数据处理说明

概要说明

降维处理

白化

算法及代码

图表和结果展现

运行环境

运行结果

参考文档

8 Responses to kaggle数字识别器训练过程

发表回复 取消回复

标签

近期评论

近期文章

朋友们

分类目录

归档

发表回复取消回复